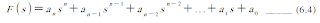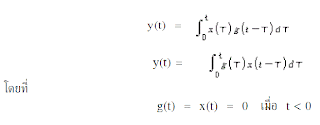1.นาย พรรษพล โฉมศิริ รหัสนิสิต 49222557
2.นายพิศิษฐ์ สิงห์โต รหัสนิสิต 49222565
3.นาย ศรีรัฐ คงหนู รหัสนิสิต 49222672
วันพุธที่ 12 พฤษภาคม พ.ศ. 2553
วันศุกร์ที่ 7 พฤษภาคม พ.ศ. 2553
Steady-State Errors
ความคลาดเคลื่อนเชิงสถิตย์ คือความแตกต่างระหว่างอินพุตและเอาต์พุต (E(s)) เมื่อป้อนสัญญาณรูปแบบต่างๆ ที่ใช้ในทดสอบเข้าไปที่อินพุตของระบบ แล้วตรวจสอบความแตกต่างที่เวลาเข้าสู่อนันต์หรือเวลาที่ระบบอยู่ในภาวะคงตัว
รูปที่ 7.1 แผนภาพระบบซึ่งมีการป้อนกลับ 1 หน่วย (unity)
ระบบที่เรานำมาตรวจสอบ Steady-State Error ต้องเป็นระบบที่เสถียรเท่านั้น ดังนั้นก่อนที่จะทำการตรวจสอบ Steady-State Error ต้องมีการตรวจสอบความเสถียรก่อนทุกครั้งและถ้าระบบไม่เสถียรจะต้องทำการปรับปรุงระบบให้เสถียรก่อนจึงจะสามารถนำมาตรวจสอบ Steady-State Error
การหา steady-state errors แสดงไว้ในรูปที่ 7.1 โดยความคลาดเคลื่อน (error) สามารถหาได้
จาก E(s) = R(s) - C(s)H(s) หรือ
Steady-State Errors หาได้จากการหาลิมิตของความคลาดเคลื่อน (e(t)) เมื่อเวลา (t) เข้าสู่อนันต์และโดยทฤษฎีค่าสุดท้ายจะได้ว่า
หรือ
ในการหา Steady-State errors มีการกำหนดอินพุตสำหรับการตรวจสอบไว้ 3 รูปแบบคือ
ลักษณะของสัญญาณที่ใช้เป็นอินพุตในการตรวจสอบ Steady-State Errors ได้แสดงไว้ในตารางที่ 6.1
การวัดค่าความคลาดเคลื่อนเชิงสถิตย์ (Evaluating Steady–State Errors)
ทำได้โดยการหาค่าความแตกต่างของระดับสัญญาณอินพุทที่ป้อนให้กับระบบ กับสัญญาณเอาต์พุตที่ได้เมื่อเวลาเข้าสู่อนันต์
พิจารณาเมื่อสัญญาณอินพุตเป็น Step function การตรวจสอบ Steady-State Error จะกระทำเมื่อเวลาเข้าสู่อนันต์หรือเมื่อระบบเข้าสู่ภาวะคงตัวแล้ว เช่นระบบอันดับ 1 สามารถวัดได้เมื่อเวลาผ่านไปอย่างน้อย 5T เมื่อ T เป็น time constant ของระบบ ดังนั้นจากรูปที่ 2(a) Steady-State Error ของระบบที่ 1 ซึ่งแสดงโดย Output 1 มีค่าเป็น 0 หรือไม่มี Steady-State Error และ Steady-StateError ของระบบที่ 2 ซึ่งแสดงโดย Output 2 มีค่าคงที่ e2(∞)
เมื่อพิจารณาสัญญาณอินพุต Ramp function จะพบว่า Steady-State Error ของระบบที่ 1 ซึ่งแสดงโดย Output 1 มีค่าเป็น 0 Steady-State Error ของระบบที่ 2 ซึ่งแสดงโดย Output 2 มีค่าคงที่ e2(∞) และ Steady-State Error ของระบบที่ 3 ซึ่งแสดงโดย Output 3 มีค่าอนันต์
ค่าความคลาดเคลื่อนเชิงสถิตย์สำหรับระบบป้อนกลับหนึ่งหน่วย
(Steady-state Error for Unity Feedback Systems)
ระบบป้อนกลับหนึ่งหน่วยแสดงได้ดังรูปที่ 7.4
ในการพิจารณาระบบควบคุมแบบป้อนกลับ เราจะมีตัวป้อนกลับ คือ H(s) ในที่นี้มีค่าเป็น 1 และมี E(s) เป็นค่าความคลาดเคลื่อนที่แท้จริงระหว่างอินพุท R(s) กับเอาต์พุต C(s) ดังนั้นเราจึงมีวิธีการหาค่าE(s) ได้จาก
เมื่อ
แทนสมการที่ 7.2 ในสมการที่ 7.1 จะได้
การตรวจสอบความคลาดเคลื่อนเชิงสถิตย์ จะทำที่เวลามีค่าเป็นอนันต์ e(∞) เราจะได้ว่า
อินพุตแบบระดับขั้น (ค่าความคลาดเคลื่อนในการควบคุมตำแหน่ง)
เมื่อสัญญาณป้อนเข้าเป็นสัญญาณ step function หนึ่งหน่วย r(t) = u(t) เมื่อแปลงลาปลาซจะได้ R(s) = 1/s แทนในสมการที่ 7.4 จะได้
หากเราต้องการให้ค่าความคลาดเคลื่อนเชิงสถิตย์มีค่าเป็นศูนย์ เราต้องออกแบบให้
อินพุทแบบลาด (ค่าความคลาดเคลื่อนในการควบคุมอัตราเร็ว)
เมื่อสัญญาณป้อนเข้าเป็นสัญญาณ ramp function r(t) = t เมื่อแปลงลาปลาซจะได้ R(s) =1/s2 แทนในสมการที่ 7.4 จะได้
หากเราต้องการให้ค่าความคลาดเคลื่อนเชิงสถิตย์มีค่าเป็นศูนย์ เราต้องออกแบบให้
อินพุทแบบพาราโบล่า (ค่าความคลาดเคลื่อนในการควบคุมอัตราเร่ง)
เมื่อสัญญาณป้อนเข้าเป็นสัญญาณ parabola function r(t) = t2 เมื่อแปลงลาปลาซจะได้ R(s)= 1/s2 แทนในสมการที่ 6.4 จะได้
หากเราต้องการให้ค่าความคลาดเคลื่อนเชิงสถิตย์มีค่าเป็นศูนย์ เราต้องออกแบบให้
ค่าคงที่ของความผิดพลาดเชิงสถิตย์และประเภทของระบบ
(Static Error Constants and System Type)
การนิยามพารามิเตอร์ต่างๆ นั้นทำให้เราสามารถที่จะนำมาใช้เพื่อระบุหาประสิทธิภาพของความคลาดเคลื่อนเชิงสถิตย์ได้ ดังเช่นที่ได้นิยามเรื่องของ damping ratio,natural frequency, setting time,percent overshoot เป็นต้น เพื่อนำไปใช้หาประสิทธิภาพของการตอบสนองชั่วขณะ (Transient response) เพื่อหาประสิทธิภาพของความคลาดเคลื่อนเชิงสถิตย์จึงต้องนิยามค่าต่างๆ เรียกว่า “Static Error Constants” ซึ่งจะนำไปใช้ในการคำนวณถัดไป
ค่าคงที่ของความผิดพลาดเชิงสถิตย์ (Static Error Constants)
ค่าความคลาดเคลื่อนเชิงสถิตย์ แสดงได้โดยสมการที่ (7.5), (7.7) และ (7.9) จะสังเกตุเห็นว่าทั้ง 3 สมการมีเทอมของส่วนที่แสดงความสัมพันธ์โดยการหาลิมิต เราจะเรียกส่วนที่มีการหาลิมิตว่า Static Error Constants ดังนี้
ประเภทของระบบ (System Type)
เมื่อสังเกตสมการคุณลักษณะของส่วน จะมีเทอมที่เป็น s คูณอยู่กับเทอมอื่นๆ ซึ่ง s ตัวนี้จะมีอยู่สามประเภทโดยแบ่งตามกำลังของตัวมันเอง ถ้าไม่มี s คูณอยู่แสดงว่าเป็น s ยกกำลัง 0 คือ 1 แบบนี้จะเป็นระบบประเภทที่ 0 ถ้า s ยกกำลัง 1 ก็จะเป็นระบบประเภทที่ 1 และถ้า s ยกกำลัง 2 ก็จะเป็นระบบ
ประเภทที่ 2 ซึ่งสามารถที่จะนำมาสรุปเป็นตารางได้ดังนี้ความสัมพันธ์ระหว่างอินพุท,ประเภทของระบบ,ค่าคงที่ของความผิดพลาดและค่าความดลาดเคลื่อนเชิงสถิตย์ดังตารางที่ 6.2 (จากหนังสืออ้างอิง [1])
เราสามารถนำเอาค่าคงที่ของความคลาดเคลื่อนไปใช้ในการระบุคุณลักษณะของค่าความเคลื่อนเชิงสถิตย์ ของระบบได้
รูปที่ 7.1 แผนภาพระบบซึ่งมีการป้อนกลับ 1 หน่วย (unity)
ระบบที่เรานำมาตรวจสอบ Steady-State Error ต้องเป็นระบบที่เสถียรเท่านั้น ดังนั้นก่อนที่จะทำการตรวจสอบ Steady-State Error ต้องมีการตรวจสอบความเสถียรก่อนทุกครั้งและถ้าระบบไม่เสถียรจะต้องทำการปรับปรุงระบบให้เสถียรก่อนจึงจะสามารถนำมาตรวจสอบ Steady-State Error
การหา steady-state errors แสดงไว้ในรูปที่ 7.1 โดยความคลาดเคลื่อน (error) สามารถหาได้
จาก E(s) = R(s) - C(s)H(s) หรือ
Steady-State Errors หาได้จากการหาลิมิตของความคลาดเคลื่อน (e(t)) เมื่อเวลา (t) เข้าสู่อนันต์และโดยทฤษฎีค่าสุดท้ายจะได้ว่า
หรือ
ในการหา Steady-State errors มีการกำหนดอินพุตสำหรับการตรวจสอบไว้ 3 รูปแบบคือ
ลักษณะของสัญญาณที่ใช้เป็นอินพุตในการตรวจสอบ Steady-State Errors ได้แสดงไว้ในตารางที่ 6.1
ตารางที่ 7.1 สัญญาณอินพุตสำหรับการทดสอบความคลาดเคลื่อนเชิงสถิตย์ (จากหนังสืออ้างอิง [1])
การวัดค่าความคลาดเคลื่อนเชิงสถิตย์ (Evaluating Steady–State Errors)
ทำได้โดยการหาค่าความแตกต่างของระดับสัญญาณอินพุทที่ป้อนให้กับระบบ กับสัญญาณเอาต์พุตที่ได้เมื่อเวลาเข้าสู่อนันต์
รูปที่ 7.2 แสดงความคลาดเคลื่อนเชิงสถิตย์สำหรับอินพุต r(t) =1 (จากหนังสืออ้างอิง [1])
พิจารณาเมื่อสัญญาณอินพุตเป็น Step function การตรวจสอบ Steady-State Error จะกระทำเมื่อเวลาเข้าสู่อนันต์หรือเมื่อระบบเข้าสู่ภาวะคงตัวแล้ว เช่นระบบอันดับ 1 สามารถวัดได้เมื่อเวลาผ่านไปอย่างน้อย 5T เมื่อ T เป็น time constant ของระบบ ดังนั้นจากรูปที่ 2(a) Steady-State Error ของระบบที่ 1 ซึ่งแสดงโดย Output 1 มีค่าเป็น 0 หรือไม่มี Steady-State Error และ Steady-StateError ของระบบที่ 2 ซึ่งแสดงโดย Output 2 มีค่าคงที่ e2(∞)
รูปที่ 7.3 แสดงความคลาดเคลื่อนเชิงสถิตย์สำหรับอินพุต r(t) = t (จากหนังสืออ้างอิง [1])
เมื่อพิจารณาสัญญาณอินพุต Ramp function จะพบว่า Steady-State Error ของระบบที่ 1 ซึ่งแสดงโดย Output 1 มีค่าเป็น 0 Steady-State Error ของระบบที่ 2 ซึ่งแสดงโดย Output 2 มีค่าคงที่ e2(∞) และ Steady-State Error ของระบบที่ 3 ซึ่งแสดงโดย Output 3 มีค่าอนันต์
ค่าความคลาดเคลื่อนเชิงสถิตย์สำหรับระบบป้อนกลับหนึ่งหน่วย
(Steady-state Error for Unity Feedback Systems)
ระบบป้อนกลับหนึ่งหน่วยแสดงได้ดังรูปที่ 7.4
รูปที่ 7.4 ระบบป้อนกลับแบบ 1 หน่วย (จากหนังสืออ้างอิง [1])
ในการพิจารณาระบบควบคุมแบบป้อนกลับ เราจะมีตัวป้อนกลับ คือ H(s) ในที่นี้มีค่าเป็น 1 และมี E(s) เป็นค่าความคลาดเคลื่อนที่แท้จริงระหว่างอินพุท R(s) กับเอาต์พุต C(s) ดังนั้นเราจึงมีวิธีการหาค่าE(s) ได้จาก
E(s) = R(s) –C(s) -- (7.1)
เมื่อ
C(s) = E(s) G(s) -- (7.2)
แทนสมการที่ 7.2 ในสมการที่ 7.1 จะได้
การตรวจสอบความคลาดเคลื่อนเชิงสถิตย์ จะทำที่เวลามีค่าเป็นอนันต์ e(∞) เราจะได้ว่า
อินพุตแบบระดับขั้น (ค่าความคลาดเคลื่อนในการควบคุมตำแหน่ง)
เมื่อสัญญาณป้อนเข้าเป็นสัญญาณ step function หนึ่งหน่วย r(t) = u(t) เมื่อแปลงลาปลาซจะได้ R(s) = 1/s แทนในสมการที่ 7.4 จะได้
หากเราต้องการให้ค่าความคลาดเคลื่อนเชิงสถิตย์มีค่าเป็นศูนย์ เราต้องออกแบบให้
อินพุทแบบลาด (ค่าความคลาดเคลื่อนในการควบคุมอัตราเร็ว)
เมื่อสัญญาณป้อนเข้าเป็นสัญญาณ ramp function r(t) = t เมื่อแปลงลาปลาซจะได้ R(s) =1/s2 แทนในสมการที่ 7.4 จะได้
หากเราต้องการให้ค่าความคลาดเคลื่อนเชิงสถิตย์มีค่าเป็นศูนย์ เราต้องออกแบบให้
อินพุทแบบพาราโบล่า (ค่าความคลาดเคลื่อนในการควบคุมอัตราเร่ง)
เมื่อสัญญาณป้อนเข้าเป็นสัญญาณ parabola function r(t) = t2 เมื่อแปลงลาปลาซจะได้ R(s)= 1/s2 แทนในสมการที่ 6.4 จะได้
หากเราต้องการให้ค่าความคลาดเคลื่อนเชิงสถิตย์มีค่าเป็นศูนย์ เราต้องออกแบบให้
ค่าคงที่ของความผิดพลาดเชิงสถิตย์และประเภทของระบบ
(Static Error Constants and System Type)
การนิยามพารามิเตอร์ต่างๆ นั้นทำให้เราสามารถที่จะนำมาใช้เพื่อระบุหาประสิทธิภาพของความคลาดเคลื่อนเชิงสถิตย์ได้ ดังเช่นที่ได้นิยามเรื่องของ damping ratio,natural frequency, setting time,percent overshoot เป็นต้น เพื่อนำไปใช้หาประสิทธิภาพของการตอบสนองชั่วขณะ (Transient response) เพื่อหาประสิทธิภาพของความคลาดเคลื่อนเชิงสถิตย์จึงต้องนิยามค่าต่างๆ เรียกว่า “Static Error Constants” ซึ่งจะนำไปใช้ในการคำนวณถัดไป
ค่าคงที่ของความผิดพลาดเชิงสถิตย์ (Static Error Constants)
ค่าความคลาดเคลื่อนเชิงสถิตย์ แสดงได้โดยสมการที่ (7.5), (7.7) และ (7.9) จะสังเกตุเห็นว่าทั้ง 3 สมการมีเทอมของส่วนที่แสดงความสัมพันธ์โดยการหาลิมิต เราจะเรียกส่วนที่มีการหาลิมิตว่า Static Error Constants ดังนี้
ประเภทของระบบ (System Type)
เมื่อสังเกตสมการคุณลักษณะของส่วน จะมีเทอมที่เป็น s คูณอยู่กับเทอมอื่นๆ ซึ่ง s ตัวนี้จะมีอยู่สามประเภทโดยแบ่งตามกำลังของตัวมันเอง ถ้าไม่มี s คูณอยู่แสดงว่าเป็น s ยกกำลัง 0 คือ 1 แบบนี้จะเป็นระบบประเภทที่ 0 ถ้า s ยกกำลัง 1 ก็จะเป็นระบบประเภทที่ 1 และถ้า s ยกกำลัง 2 ก็จะเป็นระบบ
ประเภทที่ 2 ซึ่งสามารถที่จะนำมาสรุปเป็นตารางได้ดังนี้ความสัมพันธ์ระหว่างอินพุท,ประเภทของระบบ,ค่าคงที่ของความผิดพลาดและค่าความดลาดเคลื่อนเชิงสถิตย์ดังตารางที่ 6.2 (จากหนังสืออ้างอิง [1])
ตารางที่ 6.2 แสดงประเภทของระบบและความคลาดเคลื่อนเชิงสถิตย์
เราสามารถนำเอาค่าคงที่ของความคลาดเคลื่อนไปใช้ในการระบุคุณลักษณะของค่าความเคลื่อนเชิงสถิตย์ ของระบบได้
Stability
ในการออกแบบและวิเคราะห์ระบบควบคุมสิ่งสำคัญที่เราต้องการหาคือความเสถียรของระบบ ในระบบที่ไม่เสถียรเราไม่สามารถออกแบบตัวควบคุมให้มีการตอบสนองชั่วขณะ (Transient response) หรือความผิดพลาดที่สภาวะคงที่ (Steady-state error) ตามที่ต้องการได้ ในการศึกษาในบทนี้จะจำกัดอยู่ที่ระบบ linear time-invariant
ความหมายของความเสถียรของระบบนั้นขึ้นกับจุดที่เรามองระบบ ในบทที่ผ่านมาเราได้กล่าวถึงเอาต์พุตของระบบควบคุมเกิดจากผลรวมของการตอบสนอง 2 แบบคือ ผลการตอบสนองโดยธรรมชาติ
(Natural Response) กับผลการตอบสนองโดยบังคับ (Force Response)
C(t) = Cforced(t) + Cnatural(t) _____ (6.1)
เราใช้หลักการตรวจสอบเอาต์พุตเพื่อนิยามความเสถียร (stability) ความไม่เสถียร (instability)และความเสถียรที่ขอบ (marginal stability)
การนิยามความเสถียรสำหรับระบบเชิงเส้นที่ไม่แปรตามเวลา โดยพิจารณาจากผลการตอบสนองทางธรรมชาติ (Natural response)
1. ระบบจะเป็นระบบที่เสถียรถ้าผลการตอบสนองทางธรรมชาติมีค่าประมาณศูนย์ เมื่อเวลาเข้าใกล้อนันต์
2. ระบบจะเป็นระบบที่ไม่เสถียรถ้าผลการตอบสนองทางธรรมชาติมีค่าประมาณอนันต์ ที่เวลาเข้าใกล้
อนันต์
3. ระบบจะเป็นระบบที่เสถียรแบบขอบ ถ้าผลการตอบสนองทางธรรมชาติมีค่าคงที่การนิยามความเสถียรสำหรับระบบเชิงเส้นที่ไม่แปรตามเวลา โดยพิจารณาจากเอาต์พุตเมื่อให้อินพุตที่มีขอบเขตจำกัด
a) ระบบจะเป็นระบบที่เสถียร ถ้าทุกๆอินพุต r(t) ที่มีขอบเขตจำกัดถูกป้อนเข้าไปในระบบแล้วให้เอาต์พุต c(t) ที่มีขอบเขตจำกัดออกมา
b) ระบบจะเป็นระบบที่ไม่เสถียร ถ้าทุกๆอินพุตที่มีขอบเขตจำกัดป้อนเข้าไปในระบบแล้ว ให้เอาต์พุตออกมาเป็นแบบไม่มีขอบเขต
ใน time domain เราจะเรียกว่าระบบเสถียร (stable) เมื่อเราให้อินพุต (r(t)) ที่มีค่าจำกัดแก่ระบบที่เราต้องการศึกษาและระบบนั้นให้เอาต์พุต (c(t)) ที่มีค่าจำกัดออกมาเมื่อเวลาเข้าใกล้ infinity เราจะเรียกว่าระบบไม่เสถียร (unstable) เมื่อเราให้อินพุตที่จำกัดที่มีค่าจำกัดแก่ระบบที่เราต้องการศึกษาและระบบนั้นให้เอาต์พุตที่มีค่าเป็น infinity เมื่อเวลาเข้าใกล้ infinity
ใน frequency domain เราสามารถตรวจสอบความเสถียรได้จาก transfer function
การพิจารณาความเสถียรของระบบควบคุมแบบป้อนกลับนั้นจะพิจารณาจากตำแหน่งโพลของระบบควบคุมแบบปิดที่วางอยู่ในระนาบเอส (s-plane) นั่นคือ
1. ถ้าตำแหน่งโพลอยู่ครึ่งขวาของ s-plane จำทำให้ผลตอบสนองชั่วขณะ (transient response) เพิ่มขึ้นหรือเกิดการแกว่ง (Oscillate) ตามค่าของเวลาที่เพิ่มขึ้น หมายความว่าระบบไม่เสถียร (unstable)
2. ถ้าตำแหน่งโพลอยู่ครึ่งซ้ายของ s-plane แล้วผลตอบสนองชั่วขณะ (transient response) จะเข้าสู่สภาวะคงตัว และระบบจะเสถียร
3. ถ้าตำแหน่งโพลอยู่บนแกนจินตภาพ (jw) จะทำให้ผลตอบสนอง (response) เกิดการแกว่ง (oscillate) ด้วยขนาด (amplitude) คงที่ แต่ในระบบจริงอาจจะมีสัญญาณรบกวนและทำให้เกิดการแกว่งเพิ่มของขนาด ดังนั้นในระบบควบคุมจึงไม่ควรมีโพลของลูปปิดอยู่บนแกนจินตภาพ
เราสามารถแสดงถึงขอบเขตของโพลของระบบที่ทำให้ระบบเสถียรคือด้านซ้ายของแกน jw และไม่
เสถืยรคือด้านขวาของแกน jw ได้ดังรูปที่ 5.1
เมื่อ transfer function อยู่ในรูปอัตราส่วน polynomial
Characteristic equation คือสมการที่แสดงคุณลักษณะของระบบ ซึ่งก็คือส่วนของ Transfer function, G(s) เรากำหนด characteristic equation ดังนี้
การตรวจสอบหาความเสถียรของระบบที่แสดงอยู่ในรูป polynomial โดยวิธีที่กล่าวมาด้านบน เกิดความไม่สะดวกเนื่องจากต้องทำการหาค่ารากของ characteristic equation ถ้ากำลังของcharacteristic equation สูงการหาค่ารากยิ่งยากมากขึ้น จากปัญหาดังที่กล่าวมาเราสามารถหาความเสถียรของระบบได้จากวิธีการของ Routh-Hurwitz วิธีการนี้จะบอกได้ว่ามีจำนวน pole ของระบบที่มีส่วนจริงเป็นบวกหรืออยู่อยู่ทางขวาของแกน jw ใน s-domain จำนวนกี่ pole โดยไม่จำเป็นต้องทำการหาค่ารากของ characteristic equation วิธีการของ Routh-Hurwitz นี้ไม่สามารถหาค่าของ pole ได้เพียงสามารถบอกได้ว่ามีจำนวน pole ที่มีส่วนจริงเป็นบวกจำนวนกี่ pole ส่วนจริงเป็นลบจำนวนกี่ poleและอยู่บนแกน jw ซึ่งเมื่อเราพบว่าระบบมี pole ที่มีส่วนจริงเป็นบวกเราสามารถบอกได้ว่าระบบนั้นไม่เสถียร
การสร้างตารางของ Routh สามารถศึกษาได้จากตัวอย่าง (จากหนังสืออ้างอิง [1]) สมมุติให้ระบบปิดมีทรานสเฟอร์ฟังก์ชันดังรูปด้านล่าง
Characteristic equation ของระบบคือ
การสร้างตารางของเร้าท์เริ่มต้นโดยการพิจารณาสมการคุณลักษณะ (characteristic equation) ของระบบ ทำการใส่ตัวสัมประสิทธ์ต่างเข้าไปในตารางของเร้าท์ดังนี้
ขั้นตอนในการเริ่มต้นสร้างตาราง Routh
1 ในคอลัมแรกใส่ค่า s กำลังสูงสุดของ characteristic equation ในแถวแรก แถวที่ 2 ใส่ค่า s ยกกำลังลดลง 1 และในแถวถัดๆ ไปใส่ค่า s ยกกำลังลดลงทีละ 1 เรื่อยไปจนถึง s ยกกำลังศูนย์
2 ใส่ค่าสัมประสิทธ์ของ s กำลังสูงสุดในแถวแรกคอลัมที่ 2 สัมประสิทธ์ของ s ยกกำลังลดลงที่ละ 2 ในคอลัมที่ 3, 4, ...
3 ใส่ค่าสัมประสิทธ์ของ s กำลังสูงสุดลบ 1 ในแถวที่ 2 คอลัมที่ 2 สัมประสิทธ์ของ s ยกกำลังลดลงที่ละ 2 ในคอลัมที่ 3, 4, ...
ขั้นตอนการหาค่าเพื่อเติมตาราง Routh ให้เต็มดังนี้
สมมุติให้ทรานสเฟอร์ฟังก์ชัน (Transfer function) ของระบบปิด (Closed-loop system) แสดงได้โดยสมการ (6.4) และ characteristic equation แสดงโดยสมการ (6.5)
ตารางของ Routh-Hurwitz
เมื่อ
การตรวจสอบความเสถียรจากตารางของ Routh ได้โดยการตรวจสอบที่คอลัมแรกของสัมประสิทธิ์หรือคอลัมที่ 2 ของตารางด้านบน ถ้าค่าในคอลัมนี้ไม่มีการเปลี่ยนเครื่องหมายแสดงว่าไม่มีโพลอยู่ทางขวาของ s-plane ถ้าค่าในคอลัมนี้มีการเปลี่ยนเครื่องหมายแสดงว่ามีโพลอยู่ทางขวาของ s-plane โดยที่จำนวนครั้งของการเปลี่ยนเครื่องหมายจะบอกถึงจำนวนโพลที่อยู่ทางขวาของ s-plane
กรณีพิเศษของการทดสอบแบบเร้าท์เฮอร์วิธ (Routh- Hurwitz Criterion : Special Cases)
ในบางกรณีไม่สามารถทำให้ตารางเร้าท์เฮอร์วิธสิ้นสุดลงได้ หมายความว่าไม่สามารหาค่าสัมประสิทธ์ของ s0 ได้ อันเนื่องมาจากสาเหตุดังต่อไปนี้
กรณีที่ 1 ตัวเลขเฉพาะคอลัม (Column) แรกของแถวใดแถวหนึ่งเป็นศูนย์แต่ตัวเลขอื่นในคอลัมไม่เป็นศูนย์
เมื่อตัวเลขเฉพาะคอลัมภ์แรกของแถวใดแถวหนึ่งเป็นศูนย์ จะทำให้ผลลัพธ์มีค่าเป็นอนันต์ สามารถแก้ปัญหานี้ได้โดยแทนเลขในคอลัมแรกที่เป็นศูนย์ด้วยเลขบวกที่มีค่าน้อยๆ คือ E (epsilon) ซึ่งเป็นค่าที่ใกล้ 0 มาก จะเป็นค่าบวกหรือลบก็แล้วแต่เราจะสมมุต
กรณีที่ 2 ค่าในแถว (Row) แถวใดแถวหนึ่งเป็นศูนย์ทั้งแถว
กรณีนี้เมื่อนำไปสร้างเป็นตารางแล้วเกิดเป็นศูนย์ทั้งแถว สามารถแก้ไขโดยการนำค่าในแถวอยู่บนแถวที่เป็นศูนย์ มาสร้างเป็นสมการช่วย (Auxiliary Equation) เพื่อนำสมการนั้นไปทำการดิฟเฟอร์เรนเชียลเทียบกับ s จากนั้นนำสัมประสิทธิ์ของผลลัพธ์ที่ได้จากการดิฟเฟอร์เรนเชียลมาแทนค่าลงในแถวที่เป็นศูนย์ เราก็สามารถหาค่าในตารางของเร้าท์ต่อไปได้
ความหมายของความเสถียรของระบบนั้นขึ้นกับจุดที่เรามองระบบ ในบทที่ผ่านมาเราได้กล่าวถึงเอาต์พุตของระบบควบคุมเกิดจากผลรวมของการตอบสนอง 2 แบบคือ ผลการตอบสนองโดยธรรมชาติ
(Natural Response) กับผลการตอบสนองโดยบังคับ (Force Response)
C(t) = Cforced(t) + Cnatural(t) _____ (6.1)
เราใช้หลักการตรวจสอบเอาต์พุตเพื่อนิยามความเสถียร (stability) ความไม่เสถียร (instability)และความเสถียรที่ขอบ (marginal stability)
การนิยามความเสถียรสำหรับระบบเชิงเส้นที่ไม่แปรตามเวลา โดยพิจารณาจากผลการตอบสนองทางธรรมชาติ (Natural response)
1. ระบบจะเป็นระบบที่เสถียรถ้าผลการตอบสนองทางธรรมชาติมีค่าประมาณศูนย์ เมื่อเวลาเข้าใกล้อนันต์
2. ระบบจะเป็นระบบที่ไม่เสถียรถ้าผลการตอบสนองทางธรรมชาติมีค่าประมาณอนันต์ ที่เวลาเข้าใกล้
อนันต์
3. ระบบจะเป็นระบบที่เสถียรแบบขอบ ถ้าผลการตอบสนองทางธรรมชาติมีค่าคงที่การนิยามความเสถียรสำหรับระบบเชิงเส้นที่ไม่แปรตามเวลา โดยพิจารณาจากเอาต์พุตเมื่อให้อินพุตที่มีขอบเขตจำกัด
a) ระบบจะเป็นระบบที่เสถียร ถ้าทุกๆอินพุต r(t) ที่มีขอบเขตจำกัดถูกป้อนเข้าไปในระบบแล้วให้เอาต์พุต c(t) ที่มีขอบเขตจำกัดออกมา
b) ระบบจะเป็นระบบที่ไม่เสถียร ถ้าทุกๆอินพุตที่มีขอบเขตจำกัดป้อนเข้าไปในระบบแล้ว ให้เอาต์พุตออกมาเป็นแบบไม่มีขอบเขต
ใน time domain เราจะเรียกว่าระบบเสถียร (stable) เมื่อเราให้อินพุต (r(t)) ที่มีค่าจำกัดแก่ระบบที่เราต้องการศึกษาและระบบนั้นให้เอาต์พุต (c(t)) ที่มีค่าจำกัดออกมาเมื่อเวลาเข้าใกล้ infinity เราจะเรียกว่าระบบไม่เสถียร (unstable) เมื่อเราให้อินพุตที่จำกัดที่มีค่าจำกัดแก่ระบบที่เราต้องการศึกษาและระบบนั้นให้เอาต์พุตที่มีค่าเป็น infinity เมื่อเวลาเข้าใกล้ infinity
ใน frequency domain เราสามารถตรวจสอบความเสถียรได้จาก transfer function
การพิจารณาความเสถียรของระบบควบคุมแบบป้อนกลับนั้นจะพิจารณาจากตำแหน่งโพลของระบบควบคุมแบบปิดที่วางอยู่ในระนาบเอส (s-plane) นั่นคือ
1. ถ้าตำแหน่งโพลอยู่ครึ่งขวาของ s-plane จำทำให้ผลตอบสนองชั่วขณะ (transient response) เพิ่มขึ้นหรือเกิดการแกว่ง (Oscillate) ตามค่าของเวลาที่เพิ่มขึ้น หมายความว่าระบบไม่เสถียร (unstable)
2. ถ้าตำแหน่งโพลอยู่ครึ่งซ้ายของ s-plane แล้วผลตอบสนองชั่วขณะ (transient response) จะเข้าสู่สภาวะคงตัว และระบบจะเสถียร
3. ถ้าตำแหน่งโพลอยู่บนแกนจินตภาพ (jw) จะทำให้ผลตอบสนอง (response) เกิดการแกว่ง (oscillate) ด้วยขนาด (amplitude) คงที่ แต่ในระบบจริงอาจจะมีสัญญาณรบกวนและทำให้เกิดการแกว่งเพิ่มของขนาด ดังนั้นในระบบควบคุมจึงไม่ควรมีโพลของลูปปิดอยู่บนแกนจินตภาพ
เราสามารถแสดงถึงขอบเขตของโพลของระบบที่ทำให้ระบบเสถียรคือด้านซ้ายของแกน jw และไม่
เสถืยรคือด้านขวาของแกน jw ได้ดังรูปที่ 5.1
รูปที่ 5.1 แสดงขอบเขตของตำแหน่งโพลที่ทำให้ระบบเสถียรและไม่เสถียร
เมื่อ transfer function อยู่ในรูปอัตราส่วน polynomial
Characteristic equation คือสมการที่แสดงคุณลักษณะของระบบ ซึ่งก็คือส่วนของ Transfer function, G(s) เรากำหนด characteristic equation ดังนี้
การตรวจสอบหาความเสถียรของระบบที่แสดงอยู่ในรูป polynomial โดยวิธีที่กล่าวมาด้านบน เกิดความไม่สะดวกเนื่องจากต้องทำการหาค่ารากของ characteristic equation ถ้ากำลังของcharacteristic equation สูงการหาค่ารากยิ่งยากมากขึ้น จากปัญหาดังที่กล่าวมาเราสามารถหาความเสถียรของระบบได้จากวิธีการของ Routh-Hurwitz วิธีการนี้จะบอกได้ว่ามีจำนวน pole ของระบบที่มีส่วนจริงเป็นบวกหรืออยู่อยู่ทางขวาของแกน jw ใน s-domain จำนวนกี่ pole โดยไม่จำเป็นต้องทำการหาค่ารากของ characteristic equation วิธีการของ Routh-Hurwitz นี้ไม่สามารถหาค่าของ pole ได้เพียงสามารถบอกได้ว่ามีจำนวน pole ที่มีส่วนจริงเป็นบวกจำนวนกี่ pole ส่วนจริงเป็นลบจำนวนกี่ poleและอยู่บนแกน jw ซึ่งเมื่อเราพบว่าระบบมี pole ที่มีส่วนจริงเป็นบวกเราสามารถบอกได้ว่าระบบนั้นไม่เสถียร
การสร้างตารางของ Routh สามารถศึกษาได้จากตัวอย่าง (จากหนังสืออ้างอิง [1]) สมมุติให้ระบบปิดมีทรานสเฟอร์ฟังก์ชันดังรูปด้านล่าง
Characteristic equation ของระบบคือ
การสร้างตารางของเร้าท์เริ่มต้นโดยการพิจารณาสมการคุณลักษณะ (characteristic equation) ของระบบ ทำการใส่ตัวสัมประสิทธ์ต่างเข้าไปในตารางของเร้าท์ดังนี้
ขั้นตอนในการเริ่มต้นสร้างตาราง Routh
1 ในคอลัมแรกใส่ค่า s กำลังสูงสุดของ characteristic equation ในแถวแรก แถวที่ 2 ใส่ค่า s ยกกำลังลดลง 1 และในแถวถัดๆ ไปใส่ค่า s ยกกำลังลดลงทีละ 1 เรื่อยไปจนถึง s ยกกำลังศูนย์
2 ใส่ค่าสัมประสิทธ์ของ s กำลังสูงสุดในแถวแรกคอลัมที่ 2 สัมประสิทธ์ของ s ยกกำลังลดลงที่ละ 2 ในคอลัมที่ 3, 4, ...
3 ใส่ค่าสัมประสิทธ์ของ s กำลังสูงสุดลบ 1 ในแถวที่ 2 คอลัมที่ 2 สัมประสิทธ์ของ s ยกกำลังลดลงที่ละ 2 ในคอลัมที่ 3, 4, ...
ขั้นตอนการหาค่าเพื่อเติมตาราง Routh ให้เต็มดังนี้
สมมุติให้ทรานสเฟอร์ฟังก์ชัน (Transfer function) ของระบบปิด (Closed-loop system) แสดงได้โดยสมการ (6.4) และ characteristic equation แสดงโดยสมการ (6.5)
ตารางของ Routh-Hurwitz
เมื่อ
การตรวจสอบความเสถียรจากตารางของ Routh ได้โดยการตรวจสอบที่คอลัมแรกของสัมประสิทธิ์หรือคอลัมที่ 2 ของตารางด้านบน ถ้าค่าในคอลัมนี้ไม่มีการเปลี่ยนเครื่องหมายแสดงว่าไม่มีโพลอยู่ทางขวาของ s-plane ถ้าค่าในคอลัมนี้มีการเปลี่ยนเครื่องหมายแสดงว่ามีโพลอยู่ทางขวาของ s-plane โดยที่จำนวนครั้งของการเปลี่ยนเครื่องหมายจะบอกถึงจำนวนโพลที่อยู่ทางขวาของ s-plane
กรณีพิเศษของการทดสอบแบบเร้าท์เฮอร์วิธ (Routh- Hurwitz Criterion : Special Cases)
ในบางกรณีไม่สามารถทำให้ตารางเร้าท์เฮอร์วิธสิ้นสุดลงได้ หมายความว่าไม่สามารหาค่าสัมประสิทธ์ของ s0 ได้ อันเนื่องมาจากสาเหตุดังต่อไปนี้
กรณีที่ 1 ตัวเลขเฉพาะคอลัม (Column) แรกของแถวใดแถวหนึ่งเป็นศูนย์แต่ตัวเลขอื่นในคอลัมไม่เป็นศูนย์
เมื่อตัวเลขเฉพาะคอลัมภ์แรกของแถวใดแถวหนึ่งเป็นศูนย์ จะทำให้ผลลัพธ์มีค่าเป็นอนันต์ สามารถแก้ปัญหานี้ได้โดยแทนเลขในคอลัมแรกที่เป็นศูนย์ด้วยเลขบวกที่มีค่าน้อยๆ คือ E (epsilon) ซึ่งเป็นค่าที่ใกล้ 0 มาก จะเป็นค่าบวกหรือลบก็แล้วแต่เราจะสมมุต
กรณีที่ 2 ค่าในแถว (Row) แถวใดแถวหนึ่งเป็นศูนย์ทั้งแถว
กรณีนี้เมื่อนำไปสร้างเป็นตารางแล้วเกิดเป็นศูนย์ทั้งแถว สามารถแก้ไขโดยการนำค่าในแถวอยู่บนแถวที่เป็นศูนย์ มาสร้างเป็นสมการช่วย (Auxiliary Equation) เพื่อนำสมการนั้นไปทำการดิฟเฟอร์เรนเชียลเทียบกับ s จากนั้นนำสัมประสิทธิ์ของผลลัพธ์ที่ได้จากการดิฟเฟอร์เรนเชียลมาแทนค่าลงในแถวที่เป็นศูนย์ เราก็สามารถหาค่าในตารางของเร้าท์ต่อไปได้
Reduction of Multiple Subsystem
Block diagram
Block diagram of a system is a pictorial representation of the functions performed by each component and of the flow of signal.
ข้อดีของ block diagram
– ความง่ายในการสร้างบล็อกไดอะแกรมของระบบทั้งหมด โดยเพียงการต่อบล็อกไดอะแกรมของส่วนย่อยต่างๆ ในระบบเข้าด้วยกันตามทิศทางการไหลของสัญญาณ
– สามารถทำการประเมินส่วนย่อยต่างๆ ในระบบ เพื่อหาสมรรถนะของระบบรวม
ข้อสังเกต บล็อกไดอะแกรมแสดงข้อมูลลักษณะไดนามิกของระบบ แต่ไม่ได้แสดงถึงข้อมูลโครงสร้างทางฟิสิกส์ของระบบ ดังนั้นระบบที่มีลักษณะโครงสร้างทางฟิสิกส์ไม่เหมือนกันหรือระบบที่ไม่มีความสัมพันธ์กันเลย อาจสามารถแสดงได้โดยบล็อกไดอะแกรมที่เหมือนกันComponent part of a block diagramสำหรับระบบ linear time-invariant ประกอบด้วยส่วนหลักๆ คือ signal, system, summing junction, pick off point รูปแบบพี้นฐานในการเชื่อมต่อและการลดรูปมี 3 รูปแบบคือ
1 Cascade form (a) แสดงการเชื่อมต่อ (b) แสดงระบบที่เทียบเท่า
รูปที่ 4.1 การเชื่อมต่อแบบ Cascade (จากหนังสืออ้างอิง [1])
2 Parallel form (a) แสดงการเชื่อมต่อ (b) แสดงระบบที่เทียบเท่า
รูปที่ 4.2 การเชื่อมต่อแบบ Parallel (จากหนังสืออ้างอิง [1])
3 Feedback form (a) แสดงการเชื่อมต่อ (b) แสดงระบบที่เทียบเท่า
รูปที่ 4.3 การเชื่อมต่อแบบ Feedback (จากหนังสืออ้างอิง [1])
ระบบป้อนกลับ จะนำเอาสัญญาณทางออก C(s) ป้อนกลับมายังจุดรวม (summing point) เพื่อนำไปเปรียบเทียบกับสัญญาณทางเข้า R(s) ผลการเปรียบเทียบ จะเรียกว่า สัญญาณผลต่าง (Error signal) ของระบบ สัญญาณทางออก C(s) เกิดจากผลคูณของทรานสเฟอร์ฟังก์ชัน G(s) กับสัญญาณผลต่าง E(s) ในระบบควบคุมที่เป็นเชิงเส้นใดๆ จะเขียนแทนด้วยภาพบล็อกที่ประกอบด้วยบล็อกจุดรวมและจุดแยกเมื่อสัญญาณทางออกถูกป้อนกลับไปยังจุดรวม เพื่อนำการเปรียบเทียบกับสัญญาณทางเข้านั้นจำเป็นต้องแปลงสัญญาณทางออกให้มีรูปแบบเหมือนสัญญาณทางเข้าเสียก่อน เช่น ในระบบควบคุมอุณหภูมิ สัญญาณทางออกคือ อุณหภูมิที่ถูกควบคุม (controlled temperature) สัญญาณทางเข้าเป็นแรงดันหรือกระแส จึงต้องเปลี่ยนอุณหภูมิให้อยู่ในรูปของแรงดันหรือกระแสเสียก่อนแล้วจึงนำไปเปรียบเทียบกับสัญญาณการเปลี่ยนแปลงสัญญาณนี้กระทำโดยอุปกรณ์ป้อนกลับ หรือเรียกว่า ฟังก์ชันโอนย้ายกลับ H(s) นอกจากทำหน้าที่แปลงสัญญาณทางออกแล้วยังทำหน้าที่ขยายสัญญาณนี้อีกด้วย
R(s) แทนสัญญาณทางเข้า (input signal)
C(s) แทนสัญญาณทางออก (Output signal)
E(s) แทนสัญญาณผลต่าง (Error Signal)
G(s) แทนฟังก์ชันโอนย้ายไป (Forward transfer function)
H(s) แทนฟังก์ชันโอนย้ายกลับ (Reverse transfer function)
ทรานเฟอร์ฟังก์ชันของระบบปิดหรือรูป feedback form
E(s) = R(s) ∓ C(s) H(s)
C(s) = G(s) E(s)
C(s) = G(s)[R(s) ∓ C(s)H(s)]
= G(s)R(s) ∓ G(s)H(s)C(s)
(1±G(s)H(s))C(s) = G(s)R(s)
การย้ายบล็อกมี 4 รูปแบบคือ
1 การย้ายบล็อกไปด้านซ้ายของจุดรวม (summing point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.4 การย้ายบล็อกไปด้านซ้ายของจุดรวม (จากหนังสืออ้างอิง [1])
2 การย้ายบล็อกไปด้านขวาของจุดรวม (summing point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.5 การย้ายบล็อกไปด้านขวาของจุดรวม (จากหนังสืออ้างอิง [1])
3 การย้ายบล็อกไปด้านซ้ายของจุดแยก (pickoff point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.6 การย้ายบล็อกไปด้านซ้ายของจุดรวม (จากหนังสืออ้างอิง [1])
4 การย้ายบล็อกไปด้านขวาของจุดแยก (pickoff point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.7 การย้ายบล็อกไปด้านขวาของจุดรวม (จากหนังสืออ้างอิง [1])
ในการลดรูปเราต้องตรวจสอบว่าสัญญาณเอาต์พุตของบล็อกก่อนที่จะทำการย้ายบล็อกต้องมีค่าเท่ากันทั้งก่อนย้ายและหลังย้าย ถ้าสัญญาณที่จุดนั้นไม่เท่ากันแสดงว่าการย้ายบล็อกผิดพลาดต้องทำการแก้ไข
ตัวอย่างที่ 4.1 จงลดรูปของระบบที่แสดงในรูปที่ 4.8 โดยการเคลื่อนย้ายและรวมบล็อกไดอะแกรม
รูปที่ 4.8 แสดงบล็อกไดอะแกรมของระบบในตัวอย่าง (จากหนังสืออ้างอิง [1])
ขั้นที่ 1 เคลื่อนย้าย G2(s) ไปทางด้านซ้ายของจุดแยกสัญญาณ เพื่อสร้างเป็นระบบย่อยแบบขนาน และทำการลดระบบป้อนกลับที่ประกอบอยู่ใน G3(s) กับH3(s) ผลลัพธ์นี้แสดงในรูปที่ 4.9
รูปที่ 9 เคลื่อนย้าย G2(s) ไปทางด้านซ้ายของจุดแยกสัญญาณ (จากหนังสืออ้างอิง [1])
ขั้นที่ 2 ทำการลดส่วนที่ขนานกันอยู่ของ 1/G2(s) กับสัญญาณหนึ่งหน่วย(unity) และทำการเลื่อน G1(s)ไปทางด้านขวาของจุดร่วม ซึ่งจะกลายเป็นระบบย่อยที่ขนานอยู่ในลูปป้อนกลับ ซึ่งผลลัพธ์ได้แสดงในรูปที่ 4.10
รูปที่ 4.10 ระบบหลังจากผ่านขั้นที่ 2 (จากหนังสืออ้างอิง [1])
ขั้นที่ 3 ยุบจุดร่วมด้านซ้ายที่ต่อกันอยู่สองตัวให้เป็นหนึ่งเดียว โดยการบวกบล็อกป้อนกลับทั้งสองเข้าด้วยกัน และบล็อกที่เรียงต่อกันด้านขวาก็ทำให้กลายเป็นบล็อกเดียวด้วยวิธีการเรียงต่อกันรูปที่ 4.11
รูปที่ 4.11 ระบบหลังจากผ่านขั้นที่ 3 (จากหนังสืออ้างอิง [1])
ขั้นที่ 4 ใช้สูตรของการป้อนกลับทำการลดให้เหลือบล็อกด้านซ้ายหนึ่งบล็อกตามรูปที่ 4.12
รูปที่ 4.12 ระบบหลังจากผ่านขั้นที่ 4 (จากหนังสืออ้างอิง [1])
ขั้นสุดท้าย ทำการคูณกันของบล็อกทั้งสองที่เรียงต่อเข้าด้วยกัน ซึ่งผลลัพธ์สุดท้ายแสดงในรูปที่ 4.13
รูปที่ 4.13 ระบบหลังจากทำการย่อระบบย่อย (จากหนังสืออ้างอิง [1])
Block diagram of a system is a pictorial representation of the functions performed by each component and of the flow of signal.
ข้อดีของ block diagram
– ความง่ายในการสร้างบล็อกไดอะแกรมของระบบทั้งหมด โดยเพียงการต่อบล็อกไดอะแกรมของส่วนย่อยต่างๆ ในระบบเข้าด้วยกันตามทิศทางการไหลของสัญญาณ
– สามารถทำการประเมินส่วนย่อยต่างๆ ในระบบ เพื่อหาสมรรถนะของระบบรวม
ข้อสังเกต บล็อกไดอะแกรมแสดงข้อมูลลักษณะไดนามิกของระบบ แต่ไม่ได้แสดงถึงข้อมูลโครงสร้างทางฟิสิกส์ของระบบ ดังนั้นระบบที่มีลักษณะโครงสร้างทางฟิสิกส์ไม่เหมือนกันหรือระบบที่ไม่มีความสัมพันธ์กันเลย อาจสามารถแสดงได้โดยบล็อกไดอะแกรมที่เหมือนกันComponent part of a block diagramสำหรับระบบ linear time-invariant ประกอบด้วยส่วนหลักๆ คือ signal, system, summing junction, pick off point รูปแบบพี้นฐานในการเชื่อมต่อและการลดรูปมี 3 รูปแบบคือ
1 Cascade form (a) แสดงการเชื่อมต่อ (b) แสดงระบบที่เทียบเท่า
รูปที่ 4.1 การเชื่อมต่อแบบ Cascade (จากหนังสืออ้างอิง [1])
2 Parallel form (a) แสดงการเชื่อมต่อ (b) แสดงระบบที่เทียบเท่า
รูปที่ 4.2 การเชื่อมต่อแบบ Parallel (จากหนังสืออ้างอิง [1])
3 Feedback form (a) แสดงการเชื่อมต่อ (b) แสดงระบบที่เทียบเท่า
รูปที่ 4.3 การเชื่อมต่อแบบ Feedback (จากหนังสืออ้างอิง [1])
ระบบป้อนกลับ จะนำเอาสัญญาณทางออก C(s) ป้อนกลับมายังจุดรวม (summing point) เพื่อนำไปเปรียบเทียบกับสัญญาณทางเข้า R(s) ผลการเปรียบเทียบ จะเรียกว่า สัญญาณผลต่าง (Error signal) ของระบบ สัญญาณทางออก C(s) เกิดจากผลคูณของทรานสเฟอร์ฟังก์ชัน G(s) กับสัญญาณผลต่าง E(s) ในระบบควบคุมที่เป็นเชิงเส้นใดๆ จะเขียนแทนด้วยภาพบล็อกที่ประกอบด้วยบล็อกจุดรวมและจุดแยกเมื่อสัญญาณทางออกถูกป้อนกลับไปยังจุดรวม เพื่อนำการเปรียบเทียบกับสัญญาณทางเข้านั้นจำเป็นต้องแปลงสัญญาณทางออกให้มีรูปแบบเหมือนสัญญาณทางเข้าเสียก่อน เช่น ในระบบควบคุมอุณหภูมิ สัญญาณทางออกคือ อุณหภูมิที่ถูกควบคุม (controlled temperature) สัญญาณทางเข้าเป็นแรงดันหรือกระแส จึงต้องเปลี่ยนอุณหภูมิให้อยู่ในรูปของแรงดันหรือกระแสเสียก่อนแล้วจึงนำไปเปรียบเทียบกับสัญญาณการเปลี่ยนแปลงสัญญาณนี้กระทำโดยอุปกรณ์ป้อนกลับ หรือเรียกว่า ฟังก์ชันโอนย้ายกลับ H(s) นอกจากทำหน้าที่แปลงสัญญาณทางออกแล้วยังทำหน้าที่ขยายสัญญาณนี้อีกด้วย
R(s) แทนสัญญาณทางเข้า (input signal)
C(s) แทนสัญญาณทางออก (Output signal)
E(s) แทนสัญญาณผลต่าง (Error Signal)
G(s) แทนฟังก์ชันโอนย้ายไป (Forward transfer function)
H(s) แทนฟังก์ชันโอนย้ายกลับ (Reverse transfer function)
ทรานเฟอร์ฟังก์ชันของระบบปิดหรือรูป feedback form
E(s) = R(s) ∓ C(s) H(s)
C(s) = G(s) E(s)
C(s) = G(s)[R(s) ∓ C(s)H(s)]
= G(s)R(s) ∓ G(s)H(s)C(s)
(1±G(s)H(s))C(s) = G(s)R(s)
การย้ายบล็อกมี 4 รูปแบบคือ
1 การย้ายบล็อกไปด้านซ้ายของจุดรวม (summing point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.4 การย้ายบล็อกไปด้านซ้ายของจุดรวม (จากหนังสืออ้างอิง [1])
2 การย้ายบล็อกไปด้านขวาของจุดรวม (summing point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.5 การย้ายบล็อกไปด้านขวาของจุดรวม (จากหนังสืออ้างอิง [1])
3 การย้ายบล็อกไปด้านซ้ายของจุดแยก (pickoff point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.6 การย้ายบล็อกไปด้านซ้ายของจุดรวม (จากหนังสืออ้างอิง [1])
4 การย้ายบล็อกไปด้านขวาของจุดแยก (pickoff point) แสดงรูปการเทียบเท่าได้ดังนี้
รูปที่ 4.7 การย้ายบล็อกไปด้านขวาของจุดรวม (จากหนังสืออ้างอิง [1])
ในการลดรูปเราต้องตรวจสอบว่าสัญญาณเอาต์พุตของบล็อกก่อนที่จะทำการย้ายบล็อกต้องมีค่าเท่ากันทั้งก่อนย้ายและหลังย้าย ถ้าสัญญาณที่จุดนั้นไม่เท่ากันแสดงว่าการย้ายบล็อกผิดพลาดต้องทำการแก้ไข
ตัวอย่างที่ 4.1 จงลดรูปของระบบที่แสดงในรูปที่ 4.8 โดยการเคลื่อนย้ายและรวมบล็อกไดอะแกรม
รูปที่ 4.8 แสดงบล็อกไดอะแกรมของระบบในตัวอย่าง (จากหนังสืออ้างอิง [1])
ขั้นที่ 1 เคลื่อนย้าย G2(s) ไปทางด้านซ้ายของจุดแยกสัญญาณ เพื่อสร้างเป็นระบบย่อยแบบขนาน และทำการลดระบบป้อนกลับที่ประกอบอยู่ใน G3(s) กับH3(s) ผลลัพธ์นี้แสดงในรูปที่ 4.9
รูปที่ 9 เคลื่อนย้าย G2(s) ไปทางด้านซ้ายของจุดแยกสัญญาณ (จากหนังสืออ้างอิง [1])
ขั้นที่ 2 ทำการลดส่วนที่ขนานกันอยู่ของ 1/G2(s) กับสัญญาณหนึ่งหน่วย(unity) และทำการเลื่อน G1(s)ไปทางด้านขวาของจุดร่วม ซึ่งจะกลายเป็นระบบย่อยที่ขนานอยู่ในลูปป้อนกลับ ซึ่งผลลัพธ์ได้แสดงในรูปที่ 4.10
รูปที่ 4.10 ระบบหลังจากผ่านขั้นที่ 2 (จากหนังสืออ้างอิง [1])
ขั้นที่ 3 ยุบจุดร่วมด้านซ้ายที่ต่อกันอยู่สองตัวให้เป็นหนึ่งเดียว โดยการบวกบล็อกป้อนกลับทั้งสองเข้าด้วยกัน และบล็อกที่เรียงต่อกันด้านขวาก็ทำให้กลายเป็นบล็อกเดียวด้วยวิธีการเรียงต่อกันรูปที่ 4.11
รูปที่ 4.11 ระบบหลังจากผ่านขั้นที่ 3 (จากหนังสืออ้างอิง [1])
ขั้นที่ 4 ใช้สูตรของการป้อนกลับทำการลดให้เหลือบล็อกด้านซ้ายหนึ่งบล็อกตามรูปที่ 4.12
รูปที่ 4.12 ระบบหลังจากผ่านขั้นที่ 4 (จากหนังสืออ้างอิง [1])
ขั้นสุดท้าย ทำการคูณกันของบล็อกทั้งสองที่เรียงต่อเข้าด้วยกัน ซึ่งผลลัพธ์สุดท้ายแสดงในรูปที่ 4.13
รูปที่ 4.13 ระบบหลังจากทำการย่อระบบย่อย (จากหนังสืออ้างอิง [1])
Time Response
โพลและซีโร (Pole and Zeros)
การตอบสนองด้านเอาต์พุต (output response) ของระบบ เป็นผลรวมของ การตอบสนอง 2 ชนิด
คือ force response และ natural response
force response อาจจะเรียกอีกอย่างได้ว่า steady-state response เป็นการตอบสนองเนื่องจากสัญญาณอินพุต ส่วน natural response เป็นการตอบสนองตามธรรมชาติเนื่องจากโพลของระบบ
โพล คือ ค่าของตัวแปร s ในทรานสเฟอร์ฟังก์ชันที่ทำให้ทรานสเฟอร์ฟังก์ชันมีค่าเป็น infinite หรือ ค่ารากของส่วนของทรานสเฟอร์ฟังก์ชัน
ซีโร คือ ค่าของตัวแปร s ในทรานสเฟอร์ฟังก์ชันที่ทำให้ทรานสเฟอร์ฟังก์ชันมีค่าเป็นศูนย์ หรือค่ารากของเศษของทรานสเฟอร์ฟังก์ชัน
การตอบสนองของระบบต่อ impulse function
ในการวิเคราะห์และออกแบบระบบ จะต้องมีพื้นฐานในการเปรียบเทียบผลการทำงานของระบบควบคุม พื้นฐานจะได้มาจากการทดสอบโดยการให้สัญญาณอินพุต และดูผลการตอบสนองของระบบต่างๆบรรทัดฐานการออกแบบระบบจะใช้สัญญาณหรือผลตอบสนองของระบบ การใช้สัญญาณทดสอบระบบสามารถนำมาเป็นตัวบอกได้ เพราะจะทำให้เห็นความสัมพันธ์ที่เป็นอยู่ของสัญญาณอินพุตและความสามารถในการจัดการระบบด้วยสัญญาณอินพุต สัญญาณทดสอบที่ใช้กันโดยทั่วไป คือสัญญาณอินพุตที่เป็น step function, ramp function,acceleration function, impulse functions, sinusoidal function เป็นต้น โดยวิธีการใช้ความรู้ทางด้านคณิตศาสตร์และการทดลองเข้ามาช่วยในการวิเคราะห์ระบบ ทำให้ได้รูปแบบของสัญญาณที่ง่ายในฟังก์ชันของเวลา
สำหรับระบบเชิงเส้น (linear) ทรานสเฟอร์ฟังก์ชัน (transfer function) G(s) กำหนดได้ดังต่อไปนี้
เมื่อ X(s) เป็นการแปลงลาปลาซทางด้านอินพุตและ Y(s) เป็นการแปลงลาปลาซทางด้านเอาต์พุตซึ่งมาจาก
เมื่อทำการแปลงลาปลาซผกผันจะได้
ระบบอันดับ 1 (First order systems)
ระบบอันดับหนึ่งจะเป็นระบบที่ปราศจาก Zero สามารถที่จะแสดงด้วยฟังก์ชันถ่ายโอน (Transfer function) ได้ดังในสมการที่ 1 ถ้าสัญญาณเป็นสัญญาณระดับ เมื่อ R(s) = 1/s ฟังก์ชันการถ่ายโอนคือ
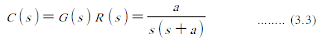
การตอบสนองของระบบแสดงไว้ในรูปที่ 3.3 การตอบสนองของระบบสิ่งที่เราสนใจที่จะศึกษาคือ rise time และ settling time
ข้อสังเกต ถ้ายิ่งค่าคงที่ของเวลา (Time constant) T = 1/a น้อยลงเท่าไหร่ระบบจะเข้าสู่ภาวะเสถียรโดยใช้เวลาน้อยลง ระบบอันดับหนึ่ง ค่อนข้างจะใช้น้อยมากแต่จะเสถียรมาก ที่จุด t=T จะได้ค่าของ C(t) เท่ากับ 0.632 หรือ 63.2% ของการเปลี่ยนแปลงทั้งหมด ลักษณะความชันของระบบจะมีค่าเท่ากับ 1/T ในที่นี้คือ a
สัญญาณความคลาดเคลื่อน e(t) หาได้จาก
1 Overdamped responses
มีโพลเป็นจำนวนจริงสองค่าที่ -σ1, -σ2 การตอบสนองทางธรรมชาติเป็นสัญญาณเอ็กโพเน็นเซียลสองตัว ที่มีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพลทั้งสอง
2 Underdamped responses 0 < ζ<1
จะมีโพลเป็นจำนวนเชิงซ้อนเป็นจำนวนเชิงซ้อนสองตัว ที่ −Wd ±j Wd การตอบสนองทางธรรมชาติเป็นการแกว่งแบบลูกคลื่นซายน์ ซึ่งมีขนาดเป็นเอ็กโพเน็นเทียลที่ค่าคงที่ของเวลามีค่าเท่ากับส่วนจริงของโพลซึ่งมีค่าลดลงตามเวลา ความถี่ของซายน์,ความถี่ของการแกว่ง มีค่าเท่ากับส่วนของจินตภาพของโพล
จะมีโพลเป็นจำนวนจริงซึ่งมีค่าซ้อนกัน 2 ค่า ที่ -σ1 การตอบสนองทางธรรมชาติมีหนึ่งเทอมที่เป็นเอ็กโพเนนเทียลซึ่งมีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพล อีกเทอมก็จะเป็นผลคูณของเวลา,t, กับเอ็กโพเนนเทียลซึ่งมีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพล
จะมีโพลมีค่าเป็นจำนวนจินตภาพสองจำนวนอยู่ที่ ±j W1 การตอบสนองทางธรรมชาติ เป็นคลื่นซายน์ซึ่งมีความถี่เท่ากับส่วนจินตภาพของโพลและมีขนาดคงที่
รูปที่ 4 การตอบสนองของระบบอันดับ 2 เมื่ออินพุตเป็น unit step ทั้ง 4 กรณี (จากหนังสืออ้างอิง [1])
ลักษณะการตอบสนองทั่วไปของระบบอันดับสอง เมื่อได้รับสัญญาณอินพุตมาตรฐานที่เป็นสัญญาณแบบอันดับหนึ่งสามารถตรวจสอบคุณสมบัติบางประการของระบบควบคุม โดยการวิเคราะห์จากค่าต่างๆ ดังนี้
1 เวลาหน่วง (Delay time, td) ปกติกำหนดจากเวลาที่ผลตอบสนองมีขนาดเป็นครึ่งหนึ่งหรือ 50% ของค่าสุดท้าย
2 เวลาไต่ขึ้น (Rise Time, tr) เป็นเวลาที่วัดจากผลตอบสนองมีขนาดเพิ่มขึ้นจาก 10% ถึง 90% หรือ 5% ถึง 95% หรือ 0% ถึง 100% ของค่าสุดท้าย สำหรับระบบควบคุมอันดับสอง ที่อยู่ในสภาวะความหน่วงน้อย (Underdamped) ปกติจะใช้ 0% ถึง 100% สำหรับระบบในสถาวะความหน่วงมาก (Overdamped) ปกติจะใช้ 10% ถึง 90%
3 เวลาสูงสุด (Peak Time , tp) คือเวลาที่ระบบควบคุมมีการตอบสนองสูงสุด หาได้จากสมการ
การตอบสนองด้านเอาต์พุต (output response) ของระบบ เป็นผลรวมของ การตอบสนอง 2 ชนิด
คือ force response และ natural response
force response อาจจะเรียกอีกอย่างได้ว่า steady-state response เป็นการตอบสนองเนื่องจากสัญญาณอินพุต ส่วน natural response เป็นการตอบสนองตามธรรมชาติเนื่องจากโพลของระบบ
โพล คือ ค่าของตัวแปร s ในทรานสเฟอร์ฟังก์ชันที่ทำให้ทรานสเฟอร์ฟังก์ชันมีค่าเป็น infinite หรือ ค่ารากของส่วนของทรานสเฟอร์ฟังก์ชัน
ซีโร คือ ค่าของตัวแปร s ในทรานสเฟอร์ฟังก์ชันที่ทำให้ทรานสเฟอร์ฟังก์ชันมีค่าเป็นศูนย์ หรือค่ารากของเศษของทรานสเฟอร์ฟังก์ชัน
การตอบสนองของระบบต่อ impulse function
ในการวิเคราะห์และออกแบบระบบ จะต้องมีพื้นฐานในการเปรียบเทียบผลการทำงานของระบบควบคุม พื้นฐานจะได้มาจากการทดสอบโดยการให้สัญญาณอินพุต และดูผลการตอบสนองของระบบต่างๆบรรทัดฐานการออกแบบระบบจะใช้สัญญาณหรือผลตอบสนองของระบบ การใช้สัญญาณทดสอบระบบสามารถนำมาเป็นตัวบอกได้ เพราะจะทำให้เห็นความสัมพันธ์ที่เป็นอยู่ของสัญญาณอินพุตและความสามารถในการจัดการระบบด้วยสัญญาณอินพุต สัญญาณทดสอบที่ใช้กันโดยทั่วไป คือสัญญาณอินพุตที่เป็น step function, ramp function,acceleration function, impulse functions, sinusoidal function เป็นต้น โดยวิธีการใช้ความรู้ทางด้านคณิตศาสตร์และการทดลองเข้ามาช่วยในการวิเคราะห์ระบบ ทำให้ได้รูปแบบของสัญญาณที่ง่ายในฟังก์ชันของเวลา
สำหรับระบบเชิงเส้น (linear) ทรานสเฟอร์ฟังก์ชัน (transfer function) G(s) กำหนดได้ดังต่อไปนี้
G(s) = Y(s) / X(s)
เมื่อ X(s) เป็นการแปลงลาปลาซทางด้านอินพุตและ Y(s) เป็นการแปลงลาปลาซทางด้านเอาต์พุตซึ่งมาจาก
Y(s) = G(s)X(s)
ดังนั้นจะได้ว่า
ผลตอบสนองของระบบที่มีอินพุตเป็น unit-impulse เมื่อค่าเริ่มต้น (initial conditions) เป็น 0 เมื่อ ค่าของการแปลงลาปลาซของ unit-impulse function มีค่าเป้น 1 หน่วย และจะได้การแปลงลาปลาซทางด้านเอาต์พุตคือ
Y(s) = G(s)
เมื่อทำการแปลงลาปลาซผกผันจะได้
y(t) = g(t) = impulse-response function
ดังนั้น g(t) (impulse-response function) เป็นผลการตอบสนองของระบบเชิงเส้น เมื่อมีอินพุตเป็น unit-impulse และค่าเริ่มต้นเป็น 0 การแปลงลาปลาซของฟังก์ชัน g(t) นี้จะประกอบด้วยลักษณะข้อมูลของระบบด้าน dynamic ฟังก์ชันที่ได้จากการแปลงลาปลาสนี้จะมีข้อมูลนี้ของระบบอยู่อย่างครบถ้วนเช่นกัน ดังนั้นเราสามารถหาการตอบสนองของระบบจากการป้อนอินพุต ระบบด้วยอินพุตที่เป็น impulse และวัดผลตอบสนองออกมาดังแสดงในรูปที่ 3.1
รูปที่ 3.1 การตอบสนองของระบบต่อสัญญาณ pulse และ impulse
ระบบอันดับ 1 (First order systems)
ระบบอันดับหนึ่งจะเป็นระบบที่ปราศจาก Zero สามารถที่จะแสดงด้วยฟังก์ชันถ่ายโอน (Transfer function) ได้ดังในสมการที่ 1 ถ้าสัญญาณเป็นสัญญาณระดับ เมื่อ R(s) = 1/s ฟังก์ชันการถ่ายโอนคือ
ทรานเฟอร์ฟังก์ชันคือ G(s) และ R(s) เป็นอินพุตแบบสัญญาณระดับ (unit step) จะสามารถหาสมการทางเอาต์พุตดังสมการที่ 3.3
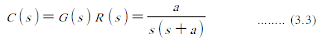
ยกเศษส่วนย่อยก็จะได้
การตอบสนองของระบบแสดงไว้ในรูปที่ 3.3 การตอบสนองของระบบสิ่งที่เราสนใจที่จะศึกษาคือ rise time และ settling time
ข้อสังเกต ถ้ายิ่งค่าคงที่ของเวลา (Time constant) T = 1/a น้อยลงเท่าไหร่ระบบจะเข้าสู่ภาวะเสถียรโดยใช้เวลาน้อยลง ระบบอันดับหนึ่ง ค่อนข้างจะใช้น้อยมากแต่จะเสถียรมาก ที่จุด t=T จะได้ค่าของ C(t) เท่ากับ 0.632 หรือ 63.2% ของการเปลี่ยนแปลงทั้งหมด ลักษณะความชันของระบบจะมีค่าเท่ากับ 1/T ในที่นี้คือ a
รูปที่ 3.3 แสดงการตอบสนอของระบบอันดับหนึ่งต่ออินพุตแบบสัญญาณระดับ (จากหนังสืออ้างอิง [1])
สัญญาณความคลาดเคลื่อน e(t) หาได้จาก
เมื่อ t เข้าสู่อนันต์แล้วค่า 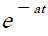 จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์
จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์
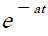 จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์
จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์ระบบอันดับสอง (Second order systems)
ระบบอันดับสองสามารถเขียนอยู่ในรูปทั่วไปได้ดังนี้
โดยที่ Wn คือความเร็วเชิงมุมในการแกว่งตามธรรมชาติ (Natural Frequency)
ζ คืออัตราการหน่วงของระบบ (damping ratio)
ζ คืออัตราการหน่วงของระบบ (damping ratio)
เราสามารถแบ่งการศึกษาเป็น 4 กรณีคือ
1 Overdamped responses
มีโพลเป็นจำนวนจริงสองค่าที่ -σ1, -σ2 การตอบสนองทางธรรมชาติเป็นสัญญาณเอ็กโพเน็นเซียลสองตัว ที่มีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพลทั้งสอง
2 Underdamped responses 0 < ζ<1
จะมีโพลเป็นจำนวนเชิงซ้อนเป็นจำนวนเชิงซ้อนสองตัว ที่ −Wd ±j Wd การตอบสนองทางธรรมชาติเป็นการแกว่งแบบลูกคลื่นซายน์ ซึ่งมีขนาดเป็นเอ็กโพเน็นเทียลที่ค่าคงที่ของเวลามีค่าเท่ากับส่วนจริงของโพลซึ่งมีค่าลดลงตามเวลา ความถี่ของซายน์,ความถี่ของการแกว่ง มีค่าเท่ากับส่วนของจินตภาพของโพล
3 Critically damped responses ζ = 1
จะมีโพลเป็นจำนวนจริงซึ่งมีค่าซ้อนกัน 2 ค่า ที่ -σ1 การตอบสนองทางธรรมชาติมีหนึ่งเทอมที่เป็นเอ็กโพเนนเทียลซึ่งมีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพล อีกเทอมก็จะเป็นผลคูณของเวลา,t, กับเอ็กโพเนนเทียลซึ่งมีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพล
4 Undamped responses ζ= 0
จะมีโพลมีค่าเป็นจำนวนจินตภาพสองจำนวนอยู่ที่ ±j W1 การตอบสนองทางธรรมชาติ เป็นคลื่นซายน์ซึ่งมีความถี่เท่ากับส่วนจินตภาพของโพลและมีขนาดคงที่
การตอบสนองของระบบและค่าต่างๆ ที่ใช้ในการกำหนดคุณสมบัติของระบบแสดงไว้ในรูปที่ 3.4 การตอบสนองในกรณี underdamped กรณี ζ ถือว่าเป็นการตอบสนองที่ดีที่สุดของระบบอันดับ 2 เนื่องจากให้ rise time และ settling time ที่ดีที่สุด
รูปที่ 4 การตอบสนองของระบบอันดับ 2 เมื่ออินพุตเป็น unit step ทั้ง 4 กรณี (จากหนังสืออ้างอิง [1])
คุณลักษณะของผลตอบสนองชั่วขณะของระบบควบคุมอันดับสอง
ลักษณะการตอบสนองทั่วไปของระบบอันดับสอง เมื่อได้รับสัญญาณอินพุตมาตรฐานที่เป็นสัญญาณแบบอันดับหนึ่งสามารถตรวจสอบคุณสมบัติบางประการของระบบควบคุม โดยการวิเคราะห์จากค่าต่างๆ ดังนี้
1 เวลาหน่วง (Delay time, td) ปกติกำหนดจากเวลาที่ผลตอบสนองมีขนาดเป็นครึ่งหนึ่งหรือ 50% ของค่าสุดท้าย
2 เวลาไต่ขึ้น (Rise Time, tr) เป็นเวลาที่วัดจากผลตอบสนองมีขนาดเพิ่มขึ้นจาก 10% ถึง 90% หรือ 5% ถึง 95% หรือ 0% ถึง 100% ของค่าสุดท้าย สำหรับระบบควบคุมอันดับสอง ที่อยู่ในสภาวะความหน่วงน้อย (Underdamped) ปกติจะใช้ 0% ถึง 100% สำหรับระบบในสถาวะความหน่วงมาก (Overdamped) ปกติจะใช้ 10% ถึง 90%
3 เวลาสูงสุด (Peak Time , tp) คือเวลาที่ระบบควบคุมมีการตอบสนองสูงสุด หาได้จากสมการ
4 ผลตอบสนองสูงสุด (Maximum Overshoot , Mp) เป็นตัวบ่งบอกถึงความคลาดเคลื่อนสูงสุดระหว่างสัญญาณอินพุทและ สัญญาณเอาท์พุตที่สภาวะของทรานเชียนท์และยังเป็นตัวช่วยวัดถึงเสถียรภาพของระบบด้วย ซึ่งจะวัดอยู่ในรูปของเปอร์เซนต์ที่เทียบจากค่าสุดท้าย
5 เวลาสู่จุดสมดุล (Settling Time, ts) เป็นเวลาที่ผลตอบสนองมีขนาดลดลงอยู่ภายในค่าที่กำหนดไว้โดยปรกติจะกำหนดเป็นค่าที่ลดลงจากค่าสุดท้าย 2% หรือ 5%
สมัครสมาชิก:
ความคิดเห็น (Atom)