ความหมายของความเสถียรของระบบนั้นขึ้นกับจุดที่เรามองระบบ ในบทที่ผ่านมาเราได้กล่าวถึงเอาต์พุตของระบบควบคุมเกิดจากผลรวมของการตอบสนอง 2 แบบคือ ผลการตอบสนองโดยธรรมชาติ
(Natural Response) กับผลการตอบสนองโดยบังคับ (Force Response)
C(t) = Cforced(t) + Cnatural(t) _____ (6.1)
เราใช้หลักการตรวจสอบเอาต์พุตเพื่อนิยามความเสถียร (stability) ความไม่เสถียร (instability)และความเสถียรที่ขอบ (marginal stability)
การนิยามความเสถียรสำหรับระบบเชิงเส้นที่ไม่แปรตามเวลา โดยพิจารณาจากผลการตอบสนองทางธรรมชาติ (Natural response)
1. ระบบจะเป็นระบบที่เสถียรถ้าผลการตอบสนองทางธรรมชาติมีค่าประมาณศูนย์ เมื่อเวลาเข้าใกล้อนันต์
2. ระบบจะเป็นระบบที่ไม่เสถียรถ้าผลการตอบสนองทางธรรมชาติมีค่าประมาณอนันต์ ที่เวลาเข้าใกล้
อนันต์
3. ระบบจะเป็นระบบที่เสถียรแบบขอบ ถ้าผลการตอบสนองทางธรรมชาติมีค่าคงที่การนิยามความเสถียรสำหรับระบบเชิงเส้นที่ไม่แปรตามเวลา โดยพิจารณาจากเอาต์พุตเมื่อให้อินพุตที่มีขอบเขตจำกัด
a) ระบบจะเป็นระบบที่เสถียร ถ้าทุกๆอินพุต r(t) ที่มีขอบเขตจำกัดถูกป้อนเข้าไปในระบบแล้วให้เอาต์พุต c(t) ที่มีขอบเขตจำกัดออกมา
b) ระบบจะเป็นระบบที่ไม่เสถียร ถ้าทุกๆอินพุตที่มีขอบเขตจำกัดป้อนเข้าไปในระบบแล้ว ให้เอาต์พุตออกมาเป็นแบบไม่มีขอบเขต
ใน time domain เราจะเรียกว่าระบบเสถียร (stable) เมื่อเราให้อินพุต (r(t)) ที่มีค่าจำกัดแก่ระบบที่เราต้องการศึกษาและระบบนั้นให้เอาต์พุต (c(t)) ที่มีค่าจำกัดออกมาเมื่อเวลาเข้าใกล้ infinity เราจะเรียกว่าระบบไม่เสถียร (unstable) เมื่อเราให้อินพุตที่จำกัดที่มีค่าจำกัดแก่ระบบที่เราต้องการศึกษาและระบบนั้นให้เอาต์พุตที่มีค่าเป็น infinity เมื่อเวลาเข้าใกล้ infinity
ใน frequency domain เราสามารถตรวจสอบความเสถียรได้จาก transfer function
การพิจารณาความเสถียรของระบบควบคุมแบบป้อนกลับนั้นจะพิจารณาจากตำแหน่งโพลของระบบควบคุมแบบปิดที่วางอยู่ในระนาบเอส (s-plane) นั่นคือ
1. ถ้าตำแหน่งโพลอยู่ครึ่งขวาของ s-plane จำทำให้ผลตอบสนองชั่วขณะ (transient response) เพิ่มขึ้นหรือเกิดการแกว่ง (Oscillate) ตามค่าของเวลาที่เพิ่มขึ้น หมายความว่าระบบไม่เสถียร (unstable)
2. ถ้าตำแหน่งโพลอยู่ครึ่งซ้ายของ s-plane แล้วผลตอบสนองชั่วขณะ (transient response) จะเข้าสู่สภาวะคงตัว และระบบจะเสถียร
3. ถ้าตำแหน่งโพลอยู่บนแกนจินตภาพ (jw) จะทำให้ผลตอบสนอง (response) เกิดการแกว่ง (oscillate) ด้วยขนาด (amplitude) คงที่ แต่ในระบบจริงอาจจะมีสัญญาณรบกวนและทำให้เกิดการแกว่งเพิ่มของขนาด ดังนั้นในระบบควบคุมจึงไม่ควรมีโพลของลูปปิดอยู่บนแกนจินตภาพ
เราสามารถแสดงถึงขอบเขตของโพลของระบบที่ทำให้ระบบเสถียรคือด้านซ้ายของแกน jw และไม่
เสถืยรคือด้านขวาของแกน jw ได้ดังรูปที่ 5.1
รูปที่ 5.1 แสดงขอบเขตของตำแหน่งโพลที่ทำให้ระบบเสถียรและไม่เสถียร
เมื่อ transfer function อยู่ในรูปอัตราส่วน polynomial
Characteristic equation คือสมการที่แสดงคุณลักษณะของระบบ ซึ่งก็คือส่วนของ Transfer function, G(s) เรากำหนด characteristic equation ดังนี้
การตรวจสอบหาความเสถียรของระบบที่แสดงอยู่ในรูป polynomial โดยวิธีที่กล่าวมาด้านบน เกิดความไม่สะดวกเนื่องจากต้องทำการหาค่ารากของ characteristic equation ถ้ากำลังของcharacteristic equation สูงการหาค่ารากยิ่งยากมากขึ้น จากปัญหาดังที่กล่าวมาเราสามารถหาความเสถียรของระบบได้จากวิธีการของ Routh-Hurwitz วิธีการนี้จะบอกได้ว่ามีจำนวน pole ของระบบที่มีส่วนจริงเป็นบวกหรืออยู่อยู่ทางขวาของแกน jw ใน s-domain จำนวนกี่ pole โดยไม่จำเป็นต้องทำการหาค่ารากของ characteristic equation วิธีการของ Routh-Hurwitz นี้ไม่สามารถหาค่าของ pole ได้เพียงสามารถบอกได้ว่ามีจำนวน pole ที่มีส่วนจริงเป็นบวกจำนวนกี่ pole ส่วนจริงเป็นลบจำนวนกี่ poleและอยู่บนแกน jw ซึ่งเมื่อเราพบว่าระบบมี pole ที่มีส่วนจริงเป็นบวกเราสามารถบอกได้ว่าระบบนั้นไม่เสถียร
การสร้างตารางของ Routh สามารถศึกษาได้จากตัวอย่าง (จากหนังสืออ้างอิง [1]) สมมุติให้ระบบปิดมีทรานสเฟอร์ฟังก์ชันดังรูปด้านล่าง
Characteristic equation ของระบบคือ
การสร้างตารางของเร้าท์เริ่มต้นโดยการพิจารณาสมการคุณลักษณะ (characteristic equation) ของระบบ ทำการใส่ตัวสัมประสิทธ์ต่างเข้าไปในตารางของเร้าท์ดังนี้
ขั้นตอนในการเริ่มต้นสร้างตาราง Routh
1 ในคอลัมแรกใส่ค่า s กำลังสูงสุดของ characteristic equation ในแถวแรก แถวที่ 2 ใส่ค่า s ยกกำลังลดลง 1 และในแถวถัดๆ ไปใส่ค่า s ยกกำลังลดลงทีละ 1 เรื่อยไปจนถึง s ยกกำลังศูนย์
2 ใส่ค่าสัมประสิทธ์ของ s กำลังสูงสุดในแถวแรกคอลัมที่ 2 สัมประสิทธ์ของ s ยกกำลังลดลงที่ละ 2 ในคอลัมที่ 3, 4, ...
3 ใส่ค่าสัมประสิทธ์ของ s กำลังสูงสุดลบ 1 ในแถวที่ 2 คอลัมที่ 2 สัมประสิทธ์ของ s ยกกำลังลดลงที่ละ 2 ในคอลัมที่ 3, 4, ...
ขั้นตอนการหาค่าเพื่อเติมตาราง Routh ให้เต็มดังนี้
สมมุติให้ทรานสเฟอร์ฟังก์ชัน (Transfer function) ของระบบปิด (Closed-loop system) แสดงได้โดยสมการ (6.4) และ characteristic equation แสดงโดยสมการ (6.5)
ตารางของ Routh-Hurwitz
เมื่อ
การตรวจสอบความเสถียรจากตารางของ Routh ได้โดยการตรวจสอบที่คอลัมแรกของสัมประสิทธิ์หรือคอลัมที่ 2 ของตารางด้านบน ถ้าค่าในคอลัมนี้ไม่มีการเปลี่ยนเครื่องหมายแสดงว่าไม่มีโพลอยู่ทางขวาของ s-plane ถ้าค่าในคอลัมนี้มีการเปลี่ยนเครื่องหมายแสดงว่ามีโพลอยู่ทางขวาของ s-plane โดยที่จำนวนครั้งของการเปลี่ยนเครื่องหมายจะบอกถึงจำนวนโพลที่อยู่ทางขวาของ s-plane
กรณีพิเศษของการทดสอบแบบเร้าท์เฮอร์วิธ (Routh- Hurwitz Criterion : Special Cases)
ในบางกรณีไม่สามารถทำให้ตารางเร้าท์เฮอร์วิธสิ้นสุดลงได้ หมายความว่าไม่สามารหาค่าสัมประสิทธ์ของ s0 ได้ อันเนื่องมาจากสาเหตุดังต่อไปนี้
กรณีที่ 1 ตัวเลขเฉพาะคอลัม (Column) แรกของแถวใดแถวหนึ่งเป็นศูนย์แต่ตัวเลขอื่นในคอลัมไม่เป็นศูนย์
เมื่อตัวเลขเฉพาะคอลัมภ์แรกของแถวใดแถวหนึ่งเป็นศูนย์ จะทำให้ผลลัพธ์มีค่าเป็นอนันต์ สามารถแก้ปัญหานี้ได้โดยแทนเลขในคอลัมแรกที่เป็นศูนย์ด้วยเลขบวกที่มีค่าน้อยๆ คือ E (epsilon) ซึ่งเป็นค่าที่ใกล้ 0 มาก จะเป็นค่าบวกหรือลบก็แล้วแต่เราจะสมมุต
กรณีที่ 2 ค่าในแถว (Row) แถวใดแถวหนึ่งเป็นศูนย์ทั้งแถว
กรณีนี้เมื่อนำไปสร้างเป็นตารางแล้วเกิดเป็นศูนย์ทั้งแถว สามารถแก้ไขโดยการนำค่าในแถวอยู่บนแถวที่เป็นศูนย์ มาสร้างเป็นสมการช่วย (Auxiliary Equation) เพื่อนำสมการนั้นไปทำการดิฟเฟอร์เรนเชียลเทียบกับ s จากนั้นนำสัมประสิทธิ์ของผลลัพธ์ที่ได้จากการดิฟเฟอร์เรนเชียลมาแทนค่าลงในแถวที่เป็นศูนย์ เราก็สามารถหาค่าในตารางของเร้าท์ต่อไปได้


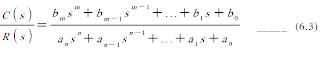
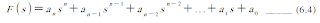






ไม่มีความคิดเห็น:
แสดงความคิดเห็น