การตอบสนองด้านเอาต์พุต (output response) ของระบบ เป็นผลรวมของ การตอบสนอง 2 ชนิด
คือ force response และ natural response
force response อาจจะเรียกอีกอย่างได้ว่า steady-state response เป็นการตอบสนองเนื่องจากสัญญาณอินพุต ส่วน natural response เป็นการตอบสนองตามธรรมชาติเนื่องจากโพลของระบบ
โพล คือ ค่าของตัวแปร s ในทรานสเฟอร์ฟังก์ชันที่ทำให้ทรานสเฟอร์ฟังก์ชันมีค่าเป็น infinite หรือ ค่ารากของส่วนของทรานสเฟอร์ฟังก์ชัน
ซีโร คือ ค่าของตัวแปร s ในทรานสเฟอร์ฟังก์ชันที่ทำให้ทรานสเฟอร์ฟังก์ชันมีค่าเป็นศูนย์ หรือค่ารากของเศษของทรานสเฟอร์ฟังก์ชัน
การตอบสนองของระบบต่อ impulse function
ในการวิเคราะห์และออกแบบระบบ จะต้องมีพื้นฐานในการเปรียบเทียบผลการทำงานของระบบควบคุม พื้นฐานจะได้มาจากการทดสอบโดยการให้สัญญาณอินพุต และดูผลการตอบสนองของระบบต่างๆบรรทัดฐานการออกแบบระบบจะใช้สัญญาณหรือผลตอบสนองของระบบ การใช้สัญญาณทดสอบระบบสามารถนำมาเป็นตัวบอกได้ เพราะจะทำให้เห็นความสัมพันธ์ที่เป็นอยู่ของสัญญาณอินพุตและความสามารถในการจัดการระบบด้วยสัญญาณอินพุต สัญญาณทดสอบที่ใช้กันโดยทั่วไป คือสัญญาณอินพุตที่เป็น step function, ramp function,acceleration function, impulse functions, sinusoidal function เป็นต้น โดยวิธีการใช้ความรู้ทางด้านคณิตศาสตร์และการทดลองเข้ามาช่วยในการวิเคราะห์ระบบ ทำให้ได้รูปแบบของสัญญาณที่ง่ายในฟังก์ชันของเวลา
สำหรับระบบเชิงเส้น (linear) ทรานสเฟอร์ฟังก์ชัน (transfer function) G(s) กำหนดได้ดังต่อไปนี้
G(s) = Y(s) / X(s)
เมื่อ X(s) เป็นการแปลงลาปลาซทางด้านอินพุตและ Y(s) เป็นการแปลงลาปลาซทางด้านเอาต์พุตซึ่งมาจาก
Y(s) = G(s)X(s)
ดังนั้นจะได้ว่า
ผลตอบสนองของระบบที่มีอินพุตเป็น unit-impulse เมื่อค่าเริ่มต้น (initial conditions) เป็น 0 เมื่อ ค่าของการแปลงลาปลาซของ unit-impulse function มีค่าเป้น 1 หน่วย และจะได้การแปลงลาปลาซทางด้านเอาต์พุตคือ
Y(s) = G(s)
เมื่อทำการแปลงลาปลาซผกผันจะได้
y(t) = g(t) = impulse-response function
ดังนั้น g(t) (impulse-response function) เป็นผลการตอบสนองของระบบเชิงเส้น เมื่อมีอินพุตเป็น unit-impulse และค่าเริ่มต้นเป็น 0 การแปลงลาปลาซของฟังก์ชัน g(t) นี้จะประกอบด้วยลักษณะข้อมูลของระบบด้าน dynamic ฟังก์ชันที่ได้จากการแปลงลาปลาสนี้จะมีข้อมูลนี้ของระบบอยู่อย่างครบถ้วนเช่นกัน ดังนั้นเราสามารถหาการตอบสนองของระบบจากการป้อนอินพุต ระบบด้วยอินพุตที่เป็น impulse และวัดผลตอบสนองออกมาดังแสดงในรูปที่ 3.1
รูปที่ 3.1 การตอบสนองของระบบต่อสัญญาณ pulse และ impulse
ระบบอันดับ 1 (First order systems)
ระบบอันดับหนึ่งจะเป็นระบบที่ปราศจาก Zero สามารถที่จะแสดงด้วยฟังก์ชันถ่ายโอน (Transfer function) ได้ดังในสมการที่ 1 ถ้าสัญญาณเป็นสัญญาณระดับ เมื่อ R(s) = 1/s ฟังก์ชันการถ่ายโอนคือ
ทรานเฟอร์ฟังก์ชันคือ G(s) และ R(s) เป็นอินพุตแบบสัญญาณระดับ (unit step) จะสามารถหาสมการทางเอาต์พุตดังสมการที่ 3.3
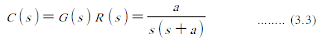
ยกเศษส่วนย่อยก็จะได้
การตอบสนองของระบบแสดงไว้ในรูปที่ 3.3 การตอบสนองของระบบสิ่งที่เราสนใจที่จะศึกษาคือ rise time และ settling time
ข้อสังเกต ถ้ายิ่งค่าคงที่ของเวลา (Time constant) T = 1/a น้อยลงเท่าไหร่ระบบจะเข้าสู่ภาวะเสถียรโดยใช้เวลาน้อยลง ระบบอันดับหนึ่ง ค่อนข้างจะใช้น้อยมากแต่จะเสถียรมาก ที่จุด t=T จะได้ค่าของ C(t) เท่ากับ 0.632 หรือ 63.2% ของการเปลี่ยนแปลงทั้งหมด ลักษณะความชันของระบบจะมีค่าเท่ากับ 1/T ในที่นี้คือ a
รูปที่ 3.3 แสดงการตอบสนอของระบบอันดับหนึ่งต่ออินพุตแบบสัญญาณระดับ (จากหนังสืออ้างอิง [1])
สัญญาณความคลาดเคลื่อน e(t) หาได้จาก
เมื่อ t เข้าสู่อนันต์แล้วค่า 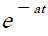 จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์
จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์
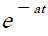 จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์
จะเข้าสู่ศูนย์นั้นคือทำให้ค่าความคลาดเคลื่อนเท่ากับศูนย์ระบบอันดับสอง (Second order systems)
ระบบอันดับสองสามารถเขียนอยู่ในรูปทั่วไปได้ดังนี้
โดยที่ Wn คือความเร็วเชิงมุมในการแกว่งตามธรรมชาติ (Natural Frequency)
ζ คืออัตราการหน่วงของระบบ (damping ratio)
ζ คืออัตราการหน่วงของระบบ (damping ratio)
เราสามารถแบ่งการศึกษาเป็น 4 กรณีคือ
1 Overdamped responses
มีโพลเป็นจำนวนจริงสองค่าที่ -σ1, -σ2 การตอบสนองทางธรรมชาติเป็นสัญญาณเอ็กโพเน็นเซียลสองตัว ที่มีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพลทั้งสอง
2 Underdamped responses 0 < ζ<1
จะมีโพลเป็นจำนวนเชิงซ้อนเป็นจำนวนเชิงซ้อนสองตัว ที่ −Wd ±j Wd การตอบสนองทางธรรมชาติเป็นการแกว่งแบบลูกคลื่นซายน์ ซึ่งมีขนาดเป็นเอ็กโพเน็นเทียลที่ค่าคงที่ของเวลามีค่าเท่ากับส่วนจริงของโพลซึ่งมีค่าลดลงตามเวลา ความถี่ของซายน์,ความถี่ของการแกว่ง มีค่าเท่ากับส่วนของจินตภาพของโพล
3 Critically damped responses ζ = 1
จะมีโพลเป็นจำนวนจริงซึ่งมีค่าซ้อนกัน 2 ค่า ที่ -σ1 การตอบสนองทางธรรมชาติมีหนึ่งเทอมที่เป็นเอ็กโพเนนเทียลซึ่งมีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพล อีกเทอมก็จะเป็นผลคูณของเวลา,t, กับเอ็กโพเนนเทียลซึ่งมีค่าคงที่ของเวลาเท่ากับส่วนกลับของค่าโพล
4 Undamped responses ζ= 0
จะมีโพลมีค่าเป็นจำนวนจินตภาพสองจำนวนอยู่ที่ ±j W1 การตอบสนองทางธรรมชาติ เป็นคลื่นซายน์ซึ่งมีความถี่เท่ากับส่วนจินตภาพของโพลและมีขนาดคงที่
การตอบสนองของระบบและค่าต่างๆ ที่ใช้ในการกำหนดคุณสมบัติของระบบแสดงไว้ในรูปที่ 3.4 การตอบสนองในกรณี underdamped กรณี ζ ถือว่าเป็นการตอบสนองที่ดีที่สุดของระบบอันดับ 2 เนื่องจากให้ rise time และ settling time ที่ดีที่สุด
รูปที่ 4 การตอบสนองของระบบอันดับ 2 เมื่ออินพุตเป็น unit step ทั้ง 4 กรณี (จากหนังสืออ้างอิง [1])
คุณลักษณะของผลตอบสนองชั่วขณะของระบบควบคุมอันดับสอง
ลักษณะการตอบสนองทั่วไปของระบบอันดับสอง เมื่อได้รับสัญญาณอินพุตมาตรฐานที่เป็นสัญญาณแบบอันดับหนึ่งสามารถตรวจสอบคุณสมบัติบางประการของระบบควบคุม โดยการวิเคราะห์จากค่าต่างๆ ดังนี้
1 เวลาหน่วง (Delay time, td) ปกติกำหนดจากเวลาที่ผลตอบสนองมีขนาดเป็นครึ่งหนึ่งหรือ 50% ของค่าสุดท้าย
2 เวลาไต่ขึ้น (Rise Time, tr) เป็นเวลาที่วัดจากผลตอบสนองมีขนาดเพิ่มขึ้นจาก 10% ถึง 90% หรือ 5% ถึง 95% หรือ 0% ถึง 100% ของค่าสุดท้าย สำหรับระบบควบคุมอันดับสอง ที่อยู่ในสภาวะความหน่วงน้อย (Underdamped) ปกติจะใช้ 0% ถึง 100% สำหรับระบบในสถาวะความหน่วงมาก (Overdamped) ปกติจะใช้ 10% ถึง 90%
3 เวลาสูงสุด (Peak Time , tp) คือเวลาที่ระบบควบคุมมีการตอบสนองสูงสุด หาได้จากสมการ
4 ผลตอบสนองสูงสุด (Maximum Overshoot , Mp) เป็นตัวบ่งบอกถึงความคลาดเคลื่อนสูงสุดระหว่างสัญญาณอินพุทและ สัญญาณเอาท์พุตที่สภาวะของทรานเชียนท์และยังเป็นตัวช่วยวัดถึงเสถียรภาพของระบบด้วย ซึ่งจะวัดอยู่ในรูปของเปอร์เซนต์ที่เทียบจากค่าสุดท้าย
5 เวลาสู่จุดสมดุล (Settling Time, ts) เป็นเวลาที่ผลตอบสนองมีขนาดลดลงอยู่ภายในค่าที่กำหนดไว้โดยปรกติจะกำหนดเป็นค่าที่ลดลงจากค่าสุดท้าย 2% หรือ 5%
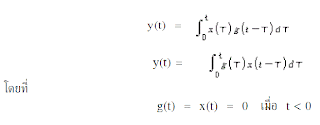















ไม่มีความคิดเห็น:
แสดงความคิดเห็น